Metroloji Kalibrasyon Ölçüm belirsizliği

METROLOJİ

Metroloji: “Ölçüm bilimidir.” Ölçüm bilimi olan metroloji, insan varlığı ile başlayan ve insanların yaşamını etkileyen, düzenleyen ve toplumun gelişimine doğrudan yön veren bir bilimdir. Toplumların gelişimine paralel olarak metroloji de zaman içinde gelişim göstermiştir.

KALİBRASYON

“Kalibrasyon: belirli koşullarda, ilk aşamada ölçüm standartları tarafından sağlanan büyüklük değerleri ve ölçüm belirsizlikleri ile bunlara karşılık gelen gösterge değerleri ve ilgili ölçüm belirsizlikleri arasında bir ilişkinin oluşturulduğu, ikinci aşamada ise bu bilginin ölçüm sonucunun göstergeden elde edilmesinde kullanıldığı işlemler dizisi” [1]

Bu tanımı açmak gerekirse, kalibrasyon kalibre edilecek cihazın (ölçüm cihazı veya fiziksel bir büyüklük üreten cihaz gibi…) bir kalibratör (izlenebilirliği sağlanmış kalibrasyon sertifikası olan ölçüm cihazı yada bir fiziksel çıkış veren cihaz gibi) ile ölçüm bölgesindeki sapmasını bulma ve bunu raporlama işlemine verilen addır. 

Örnek: Bir terazinin M1 kütle seti ile kalibrasyonunu yapmak.

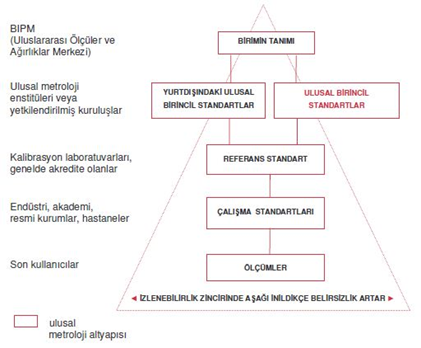
İzlenebilirlik: En kaba ölçme faaliyetinden primer seviyeye kadar olan kesintisiz ölçme işlemleri dizisidir. Kalibrasyonda izlenebilirlik olmazsa olmaz bir şarttır.

Örnek: SI birim sisteminde uzunluk ölçme birimi metredir. Metre ülkemizde primer(birincil) seviyede tanımlanması Tübitak-UME’ de gerçekleştirilmektedir.Atölyede yada fabrikada kullanılan bir şerit metrenin ulusal metroloji enstitüsündeki primer seviye standarda kadar olan kesintisiz karşılaştırma yapılması. (Kalibrasyon sertifikaları aracılığı ile)

Nominal Değer(Anma Değeri): Bir cihazın kullanımını kolaylaştırmak için cihazın çıkış veya giriş büyüklüğünün gerçek değerinin yuvarlatılmış ya da yaklaşık ifadesidir.

ÖLÇÜM BELİRSİZLİĞİ

Bir şeyin özelliğini(ne kadar uzun, ne kadar ağır…) elde edebilmek için yapılan işleme ölçüm denir. Ölçümde bir ölçüm sunucu bulunur. Ölçüm sonucu evrensellik, kendi içinde tutarlık ve taşınabilirlik gibi özellikleri taşımalıdır.

Ölçüm sonucu iki bileşenden oluşur. Beklenen Değer ve Ölçüm belirsizliği.

Ölçüm Sonucu=Beklenen Değer + Ölçüm Belirsizliği

Örnek: 15,25kg±0,12kg gibi…

Ölçüm belirsizliği, bir ölçüm sonucu hakkında var olan şüpheyi gidermek için beyan edilen değerdir.

Ölçüm hayatımızın her alanında var olan bir olgudur. Zamanın ölçülmesi, alış verişte satın aldığımız ürünlerin tartılarak ölçülmesi, arabamızın hızının ölçülmesi gibi aslında bizim yaşam konforumuzla da bu konu ilgilidir.

Ölçüm belirsizliği son 20-25 yıldır yapılan ölçümlerde, ölçüm sonucunun raporlanması ve değerlendirilmesi açısından çokça üzerinde durulan bir konudur. Bu alan da yayımlanmış birçok makale, kitap ve rehber doküman bulunmaktadır. Ölçüm belirsizliğinin hesaplanması ve raporlanmasında kullanılan en yaygın metot ISO’ nun yayınladığı GUM (Ölçümde Belirsizlik Beyanı için Rehber Doküman) (Guide to the Expression of Uncertainty in Measurement) metodudur.

GUM metodu ilk olarak BIPM, IEC, IFCC,ISO, IUPAC, IUPAP ve OIML adına 1993 yılında yayımlanmıştır.[3]

GUM metodunda tüm belirsizlikler, standart belirsizlik olarak ifade edilir. Ölçümlerdeki hata kaynaklarının standart belirsizliği A ve B tipi tahmini belirsizliklerden belirlenebilir.

Ölçüm belirsizliği hesaplamasında izlenecek yol aşağıdaki adımlarla takip edilebilir. 

GUM METODU

1. Ölçüm yönteminde kullanılan metodun model fonksiyonunu tanımla
2. Ölçüme etki eden hata kaynaklarını ve bunların dağılımlarını tanımla
3. A tipi belirsizlik Hesabının yapılması
4. B tipi belirsizlik Hesabının yapılması
5. Hata kaynaklarının etki büyüklüklerini belirlemek için duyarlılık katsayılarını belirleme
6. Birleşik Belirsizliği elde etmek için Standart belirsizlikler ile Duyarlılık Katsayıları ile birlikte hesaplanması
7. İstenen güvenililirlik seviyesi için k genişletilmiş belirsizlik katsayısı ile birleştirilmiş belirsizlik çarpılarak Genişletilmiş belirsizlik hesaplanır.

1. Ölçümün Model Fonksiyonunu Belirleme

Herhangi bir ölçüm gerçekleştirilirken ilgilenilen ölçüm büyüklüğüne, ölçümün çıkış büyüklüğü veya ölçülen, ölçülen büyüklüğü elde ederken kullanılan parametrelere de ölçümün giriş büyüklükleri denir. Ölçülen büyüklük, doğrudan ölçüm şeklinde elde edilebileceği gibi çok parametreli ölçümler şeklinde de elde edilebilir. (Örnek: Bir dikdörtgenin alanı, y=a*b, a= uzun kenarın boyu, b= kısa kenarın boyu)

Ölçüm belirsizliği hesaplamalarında yapılması gereken ilk adım ölçülen fiziksel büyüklüğün giriş parametrelerine bağlı (belirsizlik ve düzeltme bileşenlerini de içeren ) model fonksiyonunu tanımlamaktır.

Y=f(x1,x2, …xN)    Xi(i=1,2,…..N)    

Ölçüm prosedürünü tanımlayan bu matematiksel fonksiyon analitik olacağı gibi, açık bir şekilde matematiksel ifade olarak tanımlanamayacak kadar karışık fonksiyonları içerebilir, bilgisayar algoritması ve deneysel veri tipinde olabilir.

Örnek: Bir dikdörtgenin alanını ölçeceğiz. Bunu bulurken dikdörtgenin uzun kenarı ve kısa kenarı ölçülür. Bulunan değerler çarpılarak dikdörtgenin alanı bulunur.

Y=a*b         y= dikdörtgenin alanı, a=dikdörtgenin uzun kenarı, b=dikdörtgenin kısa kenarı. Bu aşamada ölçüme etki eden tüm etkileri veya hata kaynaklarını (çevresel şartlar, referans standart, ölçüm adımları, gibi…) belirlemek gerekir. Ölçüm sonucunu etkileyen bu hata kaynakları model fonksiyonda belirsizlik bileşeni veya düzeltme faktörü olarak ortaya çıkar.

2. Ölçüme Etki Eden Hata Kaynaklarını ve Dağılımlarını Belirleme

Örneğin bir kütlenin ağırlığını bir terazi ile ölçtüğümüzü düşünelim.  Ölçümlerde elde edilen sonuçlar genelde başka bir zamanda, başka bir laboratuvarda, farklı kişiler tarafından kullanılır. Bu ölçümü tekrar gerçekleştirmek ve aynı sonucu elde etmek istediğimizde bir önce ki ölçümle aynı şartların sağlanması gerekir. Fakat koşullar bir önceki ölçümde sağladığımızla hiçbir zaman birebir aynı olmayacaktır.

Herhangi bir ölçümdeki hata kaynağı, kalibratörden, kalibre edilenden cihazdan, ölçüm sisteminden, çevre şartlarından, matematiksel hesaplamadan veya operatörden kaynaklanabilir. Bu hata kaynakları sayılamayacak kadar fazla olabilir. Fakat bu hata kaynaklarının model fonksiyonda yer alıp almayacağı onun ölçüm sonucuna ne ölçüde etkilediğiyle ilgilidir. (Ör: Elektriksel kalibrasyonda termal etkiler 10E-6 mertebelerinde etkilidir. 3,5 dijit bir multimetre kalibrasyonunda bu etki göz ardı edilir ve hata kaynağı ve belirsizlik bileşeni olarak hesaba katılmaz. )   

Ölçümden ölçüme değişen bu hata kaynakları değişmekle birlikte en yaygın karşılaşılan hata kaynakları şunlardır:

• Referans Cihazın Kalibrasyon Sertifikasından gelen Belirsizlik  
• Referans Cihazın Kaymasından gelen Belirsizlik
• Tekrarlanabilirlik
• Çözünürlük Hatası
• Operatör Hatası
• Çevresel Koşullar

Referans Cihazdan Kalibrasyon Sertifikasından gelen Belirsizlik: Referans cihazımız, yani kalibratörümüzde izlenebilirliği sağlanabilmesi için bir kalibrasyon sertifikasına sahiptir. Bu kalibrasyon sertifikası elde edilirken yapılan kalibrasyonda bir belirsizlik ortaya çıkar. 

Referans Cihazdan Kaymasından gelen Belirsizlik: Referans cihazımız zamanla birlikte kendi fiziksel özelliklerinde değişimler olacaktır. (Kütlesinden birşeyler kaybetmesi, devrelerinin yaşlanması gibi….) Buda ölçümlerde hata kaynağı olarak ortaya çıkacaktır.

Tekrarlanabilirlik: Gerçekleştirilen ölçümlerde farklı zamanlarda okunan değerlerin birbirinden farklı olma veya kalibre edilen cihazın ekranındaki değerin salınması durumunda ortaya çıkar.

Tekrarlanabilirlikten gelen belirsizlik katkısı, çözünürlük belirsizliğinden gelen katkıdan çok küçükse tekrarlanabilirlik için belirsizlik hesaplamaya gerek yoktur.

Çözünürlük Hatası: Referans cihazın(kalibratör) veya Kalibre edilen cihazın çözünürlüğünden kaynaklanır. Analog ve Dijital ölçüm cihazları sınırlı hassasiyette ölçüm yapabilirler ve bunu ekranlarında sınırlı dijit olarak gösterirler. Analog cihazlarda çözünürlük en küçük bölüntü aralığı, dijital cihazlarda ise en düşük değerli hanedir.

Örnek: 3.003 V, 1347gr, 3m 15cm….

Operatör Hatası: Ölçümü gerçekleştiren personelden kaynaklanan hata kaynağıdır. Personelin yeteneği kişiden kişiye değişir. Örneğin analog cihazlardaki ölçüm değerini okuma göz yeteneği ile ilgili, kronometre kalibrasyonunda ise kişinin tepki yeteneği ile ilgilidir.

 Çevresel Koşullar: Ölçümün yapıldığı ortam ölçüm sonucunu etkiler. Çevresel etki titreşim, sıcaklık, basıç, elektriksel alan gibi çok çeşitli olabilir. Fakat bunların ölçümün hata kaynağı olarak kabul edilmesi bu etkinin hangi oranda etkilediğine bağlıdır. Eğer hesap edilebilir bir çevre etkisi ise ölçüm sonucuna düzeltme uygulanabilir. (Örnek: Bir şerit metreye termal etkilerden dolayı düzeltme uygulanabilir.)

Hesaplama Hatası: Hesaplama hatası, yapılan hesaplamalardaki yuvarlamalar, ineterpolasyonlar gibi… durumlardan kaynaklanır.

Hata Kaynakların Dağılımları

Ölçümlerde ortaya çıkan hata kaynakları yukarıdaki belirtilenler ile sınırlı değildir. Birçok şey bir ölçümü etkileyebilir. Ölçüme etki eden hata büyüklükleri rastgele değişkenler şeklinde olduğu için bu büyüklükler bir olasılıksal dağılım gösterir. Yani Model fonksiyonda sonuca etki eden hata kaynakları sonucun beklenen değerine yakın noktalarda bir dağılım gösterir. Bu dağılım hata kaynağının türüne göre birbirinden farklı olabilir. Belirsizlik Analizinde, hata kaynaklarının olasılıksal dağılımı hata değerlerinin bize hatanın olabileceği bölgenin olasılıksal dağılımını gösterir. Bu dağılım bir olasılık yoğunluk formülü ile formüle edilebilir.   

Ölçümlerde ortaya çıkabilecek hata kaynaklarının olma olasılıklarının dağılım şekilleri farklı tiplerde olabilir. Bunlar normal dağılım, dikdörtgen dağılım, üçgen dağılım, U-tipi dağılım gibi…

NOT: Birkaç tane dağılım şeklinin birleştirilmesiyle elde edilecek dağılım türü Merkezi Limit Teoremine göre normal dağılım olma eğilimindedir. Bu bilgi güvenilirlik seviyesi verirken önemlidir.

Örnek: Çözünürlüğü 0,1 V olan bir cihazdan okunan değer 5,7 V. 5.7 V değeri elde ederken bu değer 5,68’ den mi, yada 5,73’ den mi 5,7’ ye yuvarlanmıştır. Bu bilgiyi bilemeyiz. Çünkü bu bilgi çözünürlükle sınırlıdır. Bunun olma olasılığını bir grafik olarak çizersek ortaya dikdörtgen dağılım çıkacağı görülebilir.

Örnek: Sıcaklık dalgalanmasından gelen sapmalar normal(gaussian) dağılım olarak ortaya çıkar

Ölçüm büyüklüğünü elde etmede kullanılan fonksiyondaki belirsizlik bileşenleri iki grupta tanımlanabilir. A tipi ve B tipi belirsizlik değerlendirmesi.

1. A tipi belirsizlik: Standart belirsizliğin A tipi değerlendirmesi istatistiki metotlar kullanılarak hesaplanır. Genellikle tekrarlanabilirlikten gelir. A tipi değerlendirme için belirsizlik hesabı aşağıda anlatılmıştır.

• B tipi belirsizlik: Diğer hata kaynaklarından gelen belirsizlik katkısıdır. Bu hata kaynakları, geçmiş sertifikalardan gelen bilgi, cihaz çözünürlüğü, kayma, yayınlanmış dokümanlardan veya yaygın deneysel bilgilerden elde edilebilir.      

Ölçüm Sonucunda Beklenen Değeri Bulma

Bir ölçümde bir fiziki büyülük değerini(3m, 5V, 7kg…) elde ederken, operatör hatasından kaçınmak, eğer çıkış büyüklüğünde dalgalanmalar varsa daha doğru sonuç elde edebilmek için yapılan ölçümü tekrar tekrar gerçekleştirmek ölçüm ile ilgili bilgimizi artıracaktır.

Ölçüm sonucunun en iyi tahminini elde etmek, için izlenecek yol yapılan ölçümde birçok okuma yapmak ve bunların ortalamasını veya aritmetik ortalamasını almaktır. x gibi bir büyüklüğün aritmetik ortalaması x harfinin üzerine “-“ işareti konularak sembolize edilir. Pratik kural olarak genellikle 4 ile 10 arasında ölçüm sonucu almak yeterli olacaktır.

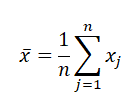
Örnek: Gerçekleştirilen bir ölçümde alınan birçok ölçüm değerinin ortalamasını bulma

Yapılan bir ölçümde 5 tane ölçüm değeri alındığını düşünelim. Bu değerler; Değerler: 12, 13, 13, 9, 10

3. A tipi Değerlendirme İçin Standart Belirsizlik Hesaplama

A tipi belirsizlik tahmini, ölçümde elde edilen farklı ölçüm sonucu değerlerinden yada tekrarlanan gözlemlerden yapılan belirsizlik tahmini olarak tanımlanır. Ölçümde elde edilen her ölçüm sonucu, birbirinden bağımsız, ölçümü temsil eden ve rastgele elde edilmesi önemlidir.

Bir ölçüm sürecinde elde edilen ve o ölçümü temsil eden rastgele ölçüm değerlerinin aritmetik ortalaması ile en iyi ölçüm sonucu elde edilmek istenir ve bu bulunan değer ölçüm sonucunun beklenen değeridir. Fakat ölçümdeki değerlerin dağılımıda ölçüm bilgisi açısından önemlidir. Bu dağılımı değerlendirmek için standart sapma kullanılır.

Standart sapma: Herhangi bir değerler kümesinin, o kümenin ortalamasından ne kadar saptığının bir ölçütüdür.

	Ölçüm Sonucu	Ortalama	Ortalamadan Sapma
1.	5,1	5,07	0,03
2.	5,0	5,07	-0,07
3.	5,2	5,07	1,03
4.	4,9	5,07	-0,17
5.	4,9	5,07	-0,17
6.	5,3	5,07	2,03

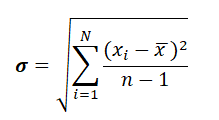
Aritmetik ortalamanın deneysel standart sapmasının en iyi tahmini değerini bulabilmek için deneysel standart sapma n gözlem sayısının kareköküne bölünür. Elde edilen değer ortalamanın deneysel standart sapması veya standart belirsizlik tir.

Standart belirsizlik bir aralıktır ve onun boyutu artı ve eksi yönde ortalamadan standart sapma kadar olan bir aralık olarak düşünülebilir.

Örnek: Yukarıdaki tablodaki verileri kullanarak hesaplama yaparsak

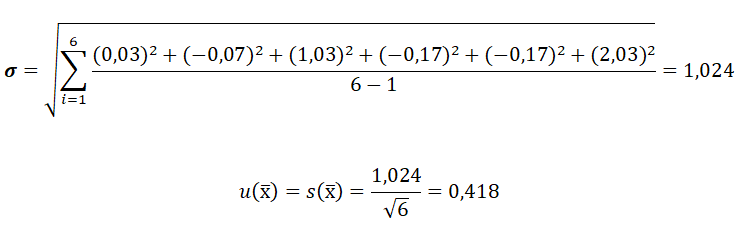
4. B tipi Değerlendirme İçin Standart Belirsizlik Hesaplama 

Bilginin daha az olduğu yerlerde (bazı B tipi belirsizlik tahminlerinde), sadece belirsizliğin alt ve üst sınırlarını belirleyebilirsiniz.  İkinci adımda belirlediğimiz hata kaynakları ve olasılık dağılım şekillerine göre standart belirsizlikler hesaplanır.

Bu belirsizlik türü üretici spesifikasyonlarından, geçmiş tecrübelerden, geçmiş ölçüm verilerinden, kullanım kitapçıklarından vb… elde edilebilir.

 (Aksiyom 1: Eğer ölçüm hataları rastgele değişkenler ise bu hatalar bir olasılık dağılımı şeklindedir.)

Eğer elimizde başka bir bilgi yoksa dağılım normal dağılım olarak seçilir.

Örnek: Dijital termometrenin çözünürlüğü 0,1 °C’ dir. Çözünürlükten gelen belirsizliği hesaplayalım

Hata kaynağı ±0,05 °C gibi bir aralıkta değişir. Yani çözünürlüğün yarısı kadar ve dağılımı o aralıkta her yerde uniform olarak dağılır. Dağılımı dikdörtgen dağılımdır.

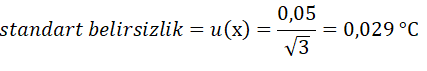
5. Hata Kaynaklarının Etki Büyüklüklerini Belirlemek İçin Duyarlılık Katsayılarını Belirleme

Ölçüm sürecinde ortaya çıkan hata kaynaklarının sonuca etkisi birbirleri ile aynı oranda olmayabilir. Hata kaynağının sonuca etki büyüklüğünü bulmak için model fonksiyonda hata kaynağına göre kısmi türevler alınarak duyarlılık katsayıları hesaplanır.

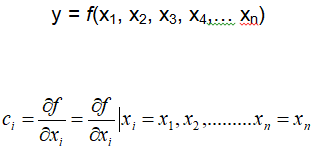
Not: Model fonksiyonu karmaşık bir yapıya sahip ve kısmi türevleri alırken zorluklar yaşanıyorsa EK1’ de alternatif yöntemde kullanılabilir.

6. Birleşik Belirsizliği elde etmek için Standart belirsizlikler ile Duyarlılık Katsayıları ile birlikte hesaplanması

Birleşik belirisizlik, hesaplanan standart belirsizlikler ile duyarlılık katsayılarının çarpımlarının karelerinin toplamının karekökü alınarak bulunur.

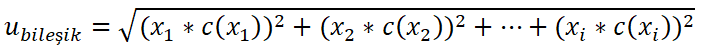
7. Genişletilmiş Belirsizliği bulmak için k genişletme katsayısı ile çarpılması

Kapsam faktörünün değeri hedeflenen güvenilirlik düzeyine göre seçilir. Metrolojik uygulamalarda genellikle k=2 seçilir. Bu değere karşılık gelen güvenilirlik düzeyi %95,45 ‘tir.

GÜVENİLİRLİK DÜZEYİ P(%)	KAPSAM FAKTÖRÜ Kp
68,27	1
90	1,645
95	1,960
99	2,576
99,7	3

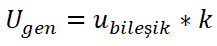
Örnek:

KAYNAKLAR

1. International vocabulary of metrology —Basic and general concepts and associated terms (VIM)
2. Metrology in short, July 2008, Preben Howarth, Fiona Redgrave
3. EA-4/02
4. NASA HANDBOOK
5. The Expression of Uncertainty and Confidence in Measurement JH 2012,UKAS